Binom Dağılımının Poisson Dağılımına Yakınsaması

Binom Dağılımının Poisson Dağılımına Yakınsaması kısmına geçmeden önce kısaca bu dağılımlardan bahsetmek en doğrusu olacaktır.

Binom Dağılımı

n tane bağımsız aynı başarı olasılığı p‘ye sahip olan Bernoulli denemesinin gerçekleştiğini farz edelim. X’e de başarılı deneme sayısı diyelim. Bu durumda X’in dağılımı parametreleri n ve p olan Binom dağılımı olacaktır.

Binom Dağılımı Olasılık Kütle Fonksiyonu (Binomial Probabilty Mass Function(PMF))

n tane bağımsız Bernoulli denemesi başarı ve hatalardan oluşan bir dizi oluşturur.(1 ve 0’lardan oluşan binary bir dizi de buna örnektir)

Herhangi bir dizinin k tane başarı n-k tane hata içerme olasılığı \(p^k(1-p)^{n-k}\) ‘dir. Başarıların(1’lerin) yerini seçerek kaç tane dizinin bu durumu sağladığını buluruz. Bu yüzden \(\begin{pmatrix}n\\k\\ \end{pmatrix}\) tane dizi bu koşulu sağlar. X için başarıların(1’lerin) sayısı dersek X’in PMF’i genel olarak binom dağılımın PMF’i aşağıdaki gibi olacaktır.

\[P(X=k)= \begin{pmatrix}n\\k\\ \end{pmatrix}p^k(1-p)^{n-k}\]

k = 0,1,…..n için (k bu değerlerden biri değilse \(P(X=k)=0\))

Poisson Dağılımı

Poisson dağılımı da Binom dağılımı gibi bir ayrık olasılık dağılımıdır. Genellikle çok fazla deneme sayısı olduğunda ve her bir deneme küçük gerçekleşme (başarı) ihtimaline sahip olduğunda belirli bir bölümdeki veya zaman aralığındaki başarılı olayların (denemelerin) sayısını (başarı tanımı probleme özgü olarak belirlenir) sayarken poisson dağılımını kullanırız.

Örneğin bir restorana bir saat içinde gelen müşteri sayısı rastgele değişkeni poisson dağılımına sahiptir. O saat içerisinde gelebilecek çok fazla insan vardır ama spesifik bir insanın o saat içerisinde gelme olasılığı çok düşüktür.

Poisson Dağılımı Olasılık Kütle Fonksiyonu (Poisson Probabilty Mass Function(PMF))

\(\lambda\) parametresine sahip olan bir X rastgele değişkenin Poisson olasılık dağılım fonksiyonu aşağıdaki gibidir.

\[P(X=k)= \frac{\lambda^k(e)^{-\lambda}}{k!} , k = 0,1,2,...\]

Binom Dağılımının Poisson Dağılımına Yakınsaması

n denemelerin sayısı sonsuza , her bir denemenin başarılı olma olasılığı p 0‘a yaklaşırken \(\lambda = np\) de sabit kalıyorsa X rastgele değişkenin olasılık kütle fonksiyonu (PMF) da Poisson olasılık kütle fonksiyonuna yakınsar.

Kanıt

\[\begin{aligned}P(X=k)&= \begin{pmatrix}n\\k\\ \end{pmatrix}p^k(1-p)^{n-k} \\ &= \frac{n(n-1)...(n-k+1)}{k!}\left(\frac{\lambda}{n}\right)^k \left(1 - \frac{\lambda}{n}\right)^n \left(1 - \frac{\lambda}{n}\right)^\left(-k\right) \\ &= \frac{n(n-1)...(n-k+1)}{n^k}\frac{\lambda ^ k}{k!} \left(1 - \frac{\lambda}{n}\right)^n \left(1 - \frac{\lambda}{n}\right)^\left(-k\right) \\ \end{aligned}\]

n \(\rightarrow \infty\) ve sabit bir k değeriyle

\[\displaylines{\frac{n(n-1)...(n-k+1)}{n^k} = \frac{n}{n}\frac{(n-1)}{n}...\frac{(n-k+1)}{n} \\ \lim_{n\to \infty}\frac{n}{n}\frac{(n-1)}{n}...\frac{(n-k+1)}{n} = 1 \\ \lim_{n\to \infty}\left(1 - \frac{\lambda}{n}\right)^\left(-k\right) = 1 \\ \lim_{n\to \infty}\left(1 - \frac{\lambda}{n}\right)^n = e^\left(-\lambda\right)}\]

Sonuç olarak n denemelerin sayısı sonsuza , her bir denemenin başarılı olma olasılığı p 0‘a yaklaşırken \(\lambda = np\) de sabit kalıyorsa

\[P(X=k)= \begin{pmatrix}n\\k\\ \end{pmatrix}p^k(1-p)^{n-k} \rightarrow \frac{\lambda ^ k (e^\left(-\lambda\right))}{k!}\]

Uygulama Bazlı Sezgisel Kanıt

# -*- coding: utf-8 -*-
"""
Created on Wed Jun 22 16:55:04 2022

@author: efemuratucarli
"""

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

#np = lambda and n = 10000 p = 0.001
poisson = np.random.poisson(lam=10, size = 3000)
n, p = 1000, 0.01
binomial = np.random.binomial(n, p, 3000)

sns.kdeplot(binomial,label="binomial")
sns.kdeplot(poisson,label="poisson")
plt.legend()
plt.show()

#np = lambda and n = 1000000000 p = 0.00000001
poisson = np.random.poisson(lam=10, size = 3000)
n, p = 1000000000, 0.00000001
binomial = np.random.binomial(n, p, 3000)

sns.kdeplot(binomial,label="binomial")
sns.kdeplot(poisson,label="poisson")
plt.legend()
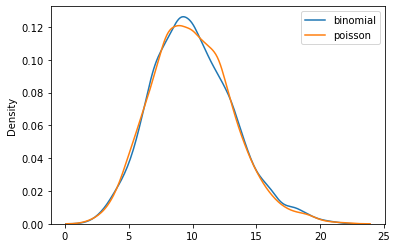
plt.show()

\(n = 1000 , p = 0.01\) iken

\(n = 1000000000 , p = 0.00000001\) iken

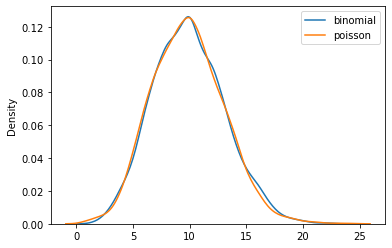
Grafiklerden ve teorik kanıttan da göreceğimiz üzere n sonsuza p 0’a yaklaşırken aynı zamanda \(np = \lambda\) korunuyorsa binom dağılımı da poisson dağılımına yakınsıyor. Ayrıca \(n = 1000 , p = 0.01\) iken dahi binom dağılımının poisson dağılımına oldukça yakın sonuçlar verdiğini de görüyoruz. Bu yüzden n görece büyük bir sayısal değere p ise görece küçük bir sayısal değere sahipken poisson olasılık kütle fonksiyonundan elde edilen değerler binom olasılık kütle fonksiyonundan elde edilen gerçek değerlere oldukça yakındır. Binom dağılımının hesaplanmasının zor olduğu kimi durumlarda bu yüzden poisson dağılımını kullanıp gerçek değere oldukça yakın değerler elde edebiliriz.